Diversos fatores contribuem para explicar o advento da Ciência de Dados, em particular sobre o desenvolvimento de modelos preditivos. Trata-se de um campo que deixou de ser considerado nichado na última década para ter sua importância reconhecida no meio empresarial, e ainda com tendência de crescimento nos próximos anos. Segundo o Departamento de Estatística do Trabalho dos Estados Unidos, projeta-se um crescimento acima de 30% do emprego neste campo entre 2021 e 2031.
Entre os fatores comumente abordados para explicar essa ascensão, consta a proliferação de linguagens de programação e recursos computacionais, que ampliaram o acesso às tecnologias demandadas para a execução de serviços dessa natureza. O acesso amplo a grandes massas de dados e ferramentas de análises é referido como democratização dos dados. Talvez a Ciência de Dados seja uma das poucas Ciências em que todos podem ter um laboratório em casa, pois basta um computador para realizar seus experimentos.
O impacto sobre a tomada de decisão
Em meio a tantos recursos e ferramentas disponíveis, convém perguntar: como podemos mensurar, efetivamente, o ganho em termos de assertividade da informação ao adotar um modelo preditivo para suporte à tomada de decisão? Uma resposta válida é confrontar o desempenho deste modelo com o procedimento previamente adotado para tomada de decisão em cenários de incerteza.
Imagine a seguinte situação: você sabe que será promovido no seu emprego, mas não sabe exatamente quando. Você pretende trocar de carro quando for promovido, e quer verificar o impacto das parcelas sobre o orçamento mensal. Mas se você não sabe quando será promovido, tampouco saberá quanto o carro estará custando no momento em que efetivar a compra. Intuitivamente, a primeira iniciativa é pesquisar o valor do carro no presente, e o utilizá-lo como referência para fazer o planejamento.
Este mecanismo, embora simples e natural, possui uma rica interpretação econômica e estatística: ele é o mais simples dos palpites sobre o valor futuro de uma variável: não há modelo matemático complexo, probabilidades, ou sequer análise qualitativa sobre o cenário prospectivo. Este processo caracteriza o que chamamos de modelo nulo: trata-se de uma representação matemática do mecanismo de formação de expectativas sobre um valor futuro na ausência de qualquer informação adicional.
A partir desta representação matemática, é possível testar a eficiência de um modelo preditivo através do confronto com dados históricos, coletando suas medidas de assertividade, comparando seu desempenho com o modelo nulo. Em meio à profusão e popularização de modelos preditivos, o modelo nulo estabelece um nível de performance mínimo desejado para qualquer outro modelo: se é verificado que meramente tomar o valor atual e supor que ele irá se repetir no futuro retorna melhor previsão que um modelo mais sofisticado, então conclui-se que este modelo não agrega para fins de antecipação do comportamento futuro de uma variável. Portanto, decisões tomadas com base neste modelo serão menos eficientes que aquelas tomadas na ausência do modelo.
Em alguns conjuntos de dados superar o modelo nulo não é um desafio trivial, e requer ferramentas e recursos avançados de Análise de Séries Temporais e Econometria. Um exemplo pode ser verificado no trabalho de Marçal e Júnior (2016). Por isso, mais importante que escolher um modelo com melhor performance dentro de um conjunto de especificações e algoritmos, é certificar-se de que ele efetivamente promove uso eficiente do conjunto informacional disponível para antecipar o comportamento futuro dos dados.
Exemplo prático
Para ilustrar o funcionamento do modelo nulo e como ele pode ser uma ferramenta útil para tarefas de previsão, utilizamos dados do preço de óleo diesel na cidade de São Paulo. Estimamos dois modelos, que vamos chamar aqui genericamente de Modelo A e Modelo B, utilizando duas técnicas distintas de Econometria de Séries Temporais e Aprendizado de Máquina, além do próprio Modelo Nulo. Simulamos os dados para representarem o comportamento passado da variável e comparamos com dados históricos para cômputo das medidas de precisão. Nesta etapa, avaliamos previsões um passo à frente: usar dados até o presente momento para predizer o valor do período imediatamente seguinte.
O tamanho da amostra que utilizamos para testar os modelos é de cerca de cem observações. Apenas para fins ilustrativos, a tabela abaixo lista os 6 primeiros valores da amostra de teste (Valor Realizado) e o valor referente à previsão sob Modelo Nulo: para cada período t, a previsão do Modelo Nulo é o valor realizado em t-1.
| Período | Valor Realizado | Modelo Nulo |
|---|---|---|
| 1 | R$ 4,20 | R$ 4,10 |
| 2 | R$ 4,14 | R$ 4,20 |
| 3 | R$ 4,20 | R$ 4,14 |
| 4 | R$ 4,18 | R$ 4,20 |
| 5 | R$ 4,24 | R$ 4,18 |
| 6 | R$ 4,15 | R$ 4,24 |
Neste exercício, vamos utilizar o Erro Absoluto Médio como medida de acurácia. Calculando o Erro Absoluto Médio para cada um dos modelos e avaliando na amostra de teste, verificamos que o Modelo A possui um Erro Absoluto Médio de 1,84%. Este valor sugere que o modelo é razoavelmente assertivo: em média, são previstos valores que desviam, para mais ou para menos, em valor inferior a 2% do realizado.
No entanto, ao avaliar o Modelo Nulo, isto é, na ausência de uma estrutura matemática ou computacional para realização das previsões, o Erro Absoluto Médio seria de 1,37%: um desempenho significativamente superior sem qualquer processo complexo de estimação. Quanto ao Modelo B, foi avaliado um erro na ordem de 1,39%, bem próximo ao Modelo Nulo, mas sem apresentar melhoria significativa. Em resumo, a melhor estratégia para prever um passo à frente, neste conjunto de dados, é meramente observar o último dado e supor que este irá se repetir no futuro.
Porém, isso não quer dizer que os modelos que estimamos não possuem validade ou utilidade. Na figura abaixo, representamos graficamente como a assertividade do Modelo B evolui em relação ao Modelo Nulo quando estendemos a análise a diferentes horizontes de previsão. Já sabemos que, para um passo à frente, o Modelo Nulo é uma boa alternativa. Mas e para mais períodos?
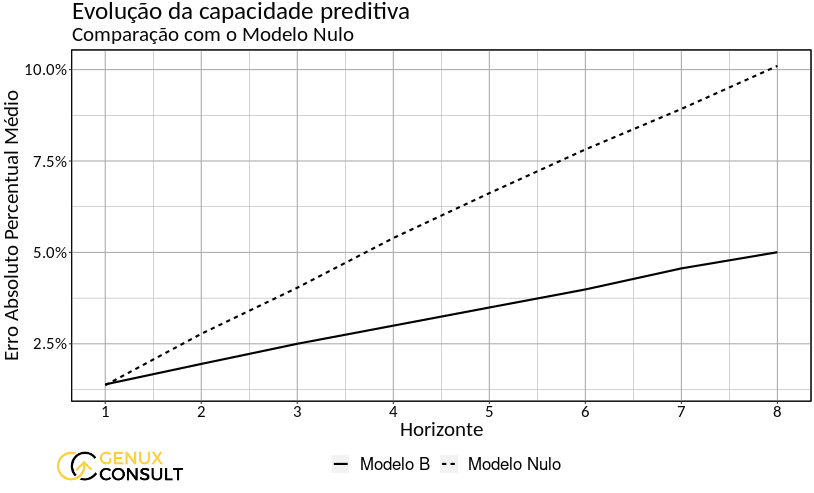
Perceba: o Modelo Nulo, embora muito eficiente no curto prazo, não é útil para previsões de períodos mais distantes. Num horizonte de tamanho 8 não é razoável supor que o preço do óleo diesel será o mesmo que no instante presente, e o ganho em termos de precisão de se adotar o Modelo B chega a 50%. Ao incorporarmos o Modelo Nulo na análise, uma ferramenta simples, detectamos uma característica importante do Modelo B, mais complexo: trata-se de um modelo mais adequado para balizar o planejamento a médio prazo.
Portanto, além da análise convencional sobre as métricas de precisão de forma isolada, é necessário verificar se a informação obtida através das previsões efetivamente aprimora a visão sobre o futuro, e qual é a melhor forma de utilizar os dados para fundamentar tomadas de decisão em horizontes de incerteza. Com a crescente oferta de dados, técnicas e recursos computacionais para previsão, é importante também desenvolver análises contextualizadas para entender o que cada uma das estatísticas obtidas revela sobre o comportamento da variável.
